Month: March 2023

最近迷上了chatGPT，逐渐得出一个结论，你使用chatGPT的效果，其实就是你和这个数字世界的边界，或者你和这个数字世界的熟悉程度。

例如

• 你只使用自然语言，那么就无法享受用机器语言和gpt聊天的乐趣；
• 局限在中文世界，chatgpt的输出范围，就要有限很多，而且会不自觉带上简中世界的特色，让你觉得在AI的多重宇宙中，无法自拔；

我越来越相信高斯分布，这个世界虽然很大，钟型曲线包裹下的芸芸众生，差异其实很小。而一旦你发现自己和长尾集合中的某个现象有了交集，一定不要犹豫、不要懒惰，要努力抓着它，这是让你摆脱中轴线的唯一机会。

2019年第一次听JJ介绍大模型的时候，除了惊奇外，没有多少想法，毕竟所需要的储备知识近乎于无，而且没有任何应用场景。虽然随后的几年，自己隐隐约约觉得，AI技术是真正的工具，使用这个工具，我可以更好的认识世界、认识自己，就像小时候利用脚蹼进行自由泳的练习一样。

中间几年无非疫情、各种无关紧要的政府项目，JJ也离职去开创自己的事业，虽然短短1年多，我从他这里没有学习到任何核心技术，但是这种人与人的差距，深深影响了我对高斯分布的看法。

终于，chatGPT来了，我梦寐以求的工具，竟然以这么戏剧化的方式将临身边。

一个例子

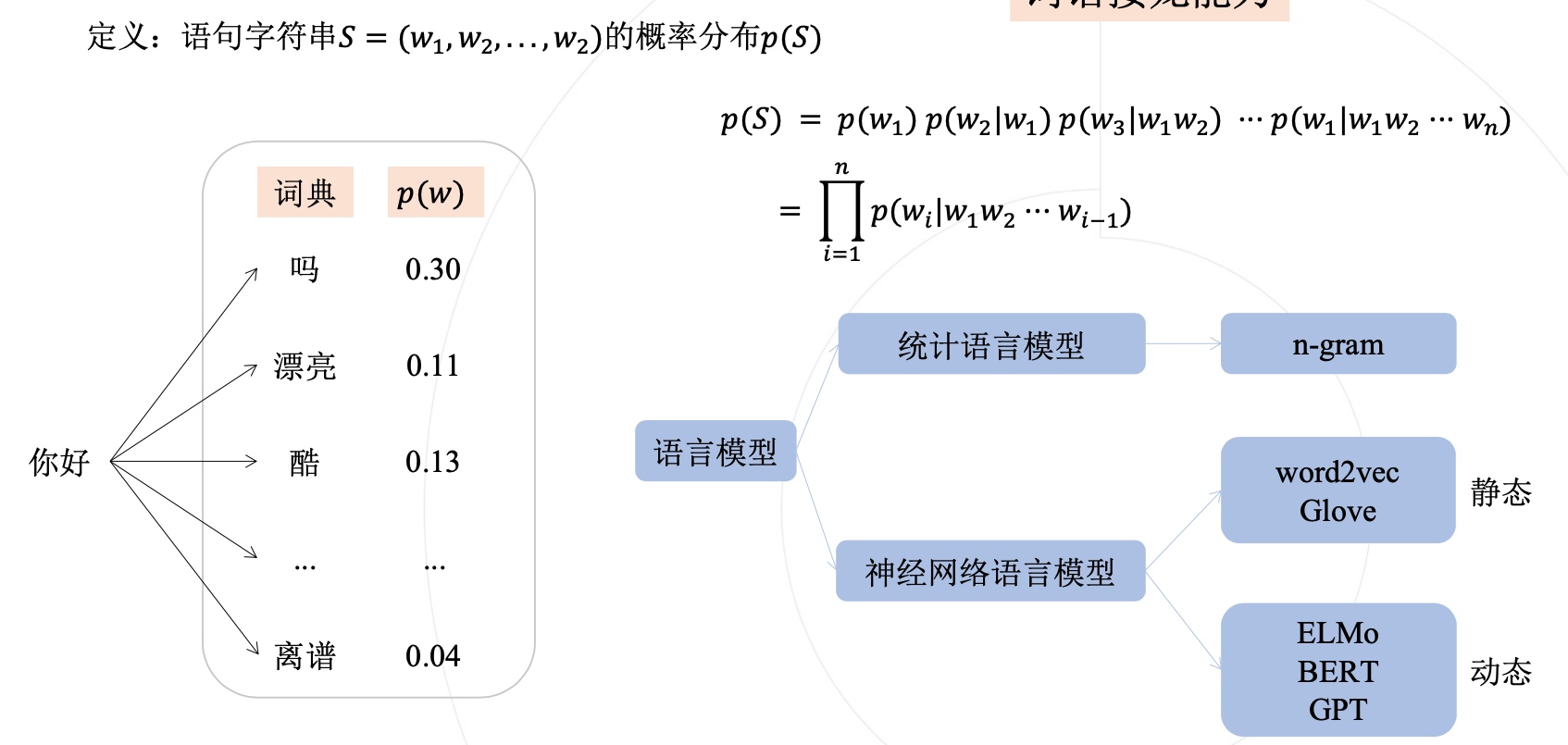
语句字符串S，就是一个句子，它的概率分布，可以是每个单词在这句话中出现的概率。

𝑝(𝑆) = 𝑝(𝑤1) 𝑝(𝑤2|𝑤1) 𝑝(𝑤3|𝑤1𝑤2) ··· 𝑝(𝑤1|𝑤1𝑤2 ··· 𝑤n)

公式的第一行，是将句子的概率分解为每个单词的条件概率相乘的形式， 例如，p(w2|w1)表示给定w1出现后，w2出现的概率。按照这样的方式，我们可以得到整个句子的概率分布。

总体来说，这个公式展示了语言模型如何基于先前的单词或文本序列，计算出下一个单词出现的概率，并进而计算整个句子的概率分布。

计算一个字符串中每个单词的出现概率可以通过以下步骤实现：

1. 将字符串S分割成单词序列w1,w2,w3,…wi。
2. 统计每个单词wi在字符串S中出现的次数。
3. 计算每个单词wi在字符串S中出现的概率，即wi出现的次数除以字符串S的总长度。
   例如，对于字符串S=“I love to eat pizza”，我们可以将其分割成单词序列[“I”, “love”, “to”, “eat”, “pizza”]。然后，我们可以统计每个单词在字符串S中出现的次数，如下所示：

• "I"出现了1次

• "love"出现了1次

• "to"出现了1次

• "eat"出现了1次

• "pizza"出现了1次
  最后，我们可以计算每个单词在字符串S中出现的概率，如下所示：

• P(“I”) = 1/5 = 0.2

• P(“love”) = 1/5 = 0.2

• P(“to”) = 1/5 = 0.2

• P(“eat”) = 1/5 = 0.2

• P(“pizza”) = 1/5 = 0.2
  这个概率分布可以用于各种自然语言处理任务，例如语言模型、机器翻译和文本分类等。

大模型训练时，面对海量数据，没法承担高昂的标注成本，往往会采用自监督学习的方式。

自监督学习是一种无监督学习的方法，它通过利用数据的某些属性来设置伪监督任务来替换标准监督任务，从而使模型能够从大量未标记的数据中进行训练。
自监督学习的目标是学习到数据的有用表示，这些表示可以用于各种任务，例如分类、检测、分割和生成等。
自监督学习的一个例子是对于“损失函数中使用到的监督信息无需人工标注”的训练范式的一种统称，自监督学习可以用在预训练上，也可以用在实际任务本身的训练上，当然目前看来还是用在预训练上的情况显著更多.

基础概念

迁移学习(Transfer Learning)使基础模型成为可能

• 技术层面上，基础模型通过转移学习(Transfer Learning)(Thrun 1998)和规模(scale)得以实现。迁移学习的思想是将从一项任务中学习到的“知识”(例如，图像中的对象识别)应用于另一项任务(例如，视频中的活动识别)。
• 在深度学习中，预训练又是迁移学习的主要方法:在替代任务上训练模型(通常只是达到目的的一种手段)，然后通过微调来适应感兴趣的下游任务。转移学习(Transfer Learning)使基础模型成为可能。

大规模化(scale)使基础模型更强大，因而GPT模型得以形成

• 大规模需要三个要素:
  • (i)计算机硬件的改进——例如，GPU吞吐量和内存在过去四年中增加了10倍;
  • (ii)Transformer模型架构的开发( Vaswani et al. 2017 )，该架构利用硬件的并行性来训练比以前更具表现力的模型;
  • 以及(iii)更多训练数据的可用性。
• 基于Transformer的序列建模方法现在应用于文本、图像、语音、表格数据、蛋白质序列、有机分子和强化学习等，这些例子的逐步形成使得使用一套统一的工具来开发各种模态的基础模型这种理念得以成熟。例如，GPT-3( Brown et al. 2020 )与GPT-2的15亿参数相比， GPT-3具有1750亿个参数，允许上下文学习，在上下文学习中，只需向下游任务提供提示(任务的自然语言描述)，语言模型就可以适应下游任务，这是产生的一种新兴属性。

Transformer奠定了生成式AI领域的游戏规则

Transformer摆脱了人工标注数据集的缺陷，模型在质量上更优、 更易于并行化，所需训练时间明显更少，
Transformer通过成功地将其应用于具有大量和有限训练数据的分析，可以很好地推广到其他任务。

• 2017年，在Ashish Vaswani et.al 的论文《Attention Is All You Need》 中，考虑到主导序列转导模型基于编码器-解码器配置中的复杂递归或卷积 神经网络，性能最好的模型被证明还是通过注意力机制(attention mechanism)连接编码器和解码器，因而《Attention Is All You Need》 中提出了一种新的简单架构——Transformer，它完全基于注意力机制， 完全不用重复和卷积，因而这些模型在质量上更优，同时更易于并行化，并 且需要的训练时间明显更少。
• Transformer出现以后，迅速取代了RNN系列变种，跻身主流模型架构基 础。(RNN缺陷正在于流水线式的顺序计算)

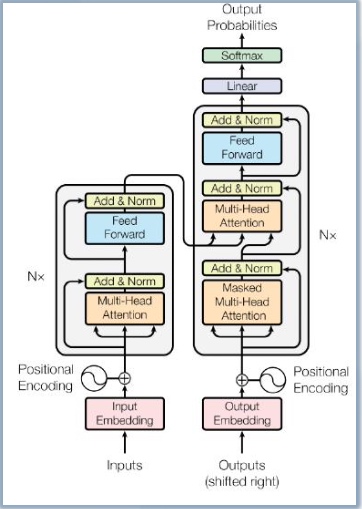
Transformer模型架构如下图